
Учитель математики
Зысь Елена Жановна,
МБОУ «Строевская СОШ»

Задачи:
- На доказательство того, что отмеченный на рисунке угол является линейным.
- На выделение линейного угла среди нескольких обозначенных на рисунке углов.
- На построение линейного угла данного двугранного угла.
- Вычислительные задачи.
Первая группа.
меню
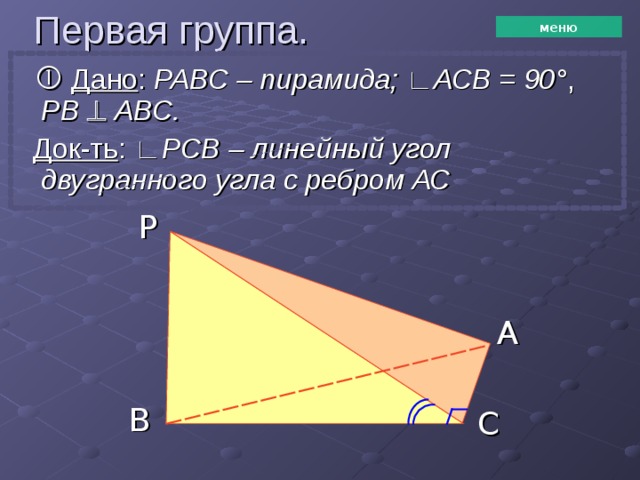
Дано : РАВС – пирамида; ∟АСВ = 90 ° , РВ АВС.
Док-ть : ∟РСВ – линейный угол двугранного угла с ребром АС
P
A
B
C
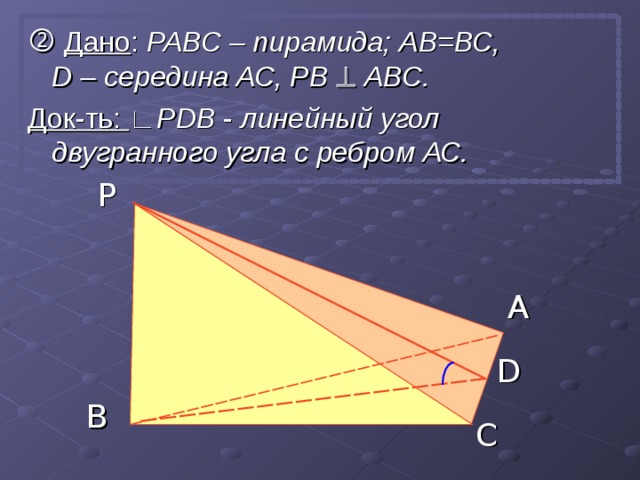
Дано : РАВС – пирамида; АВ=ВС, D – середина АС, РВ АВС.
Док-ть: ∟Р D В — линейный угол двугранного угла с ребром АС.
P
A
D
B
C
P
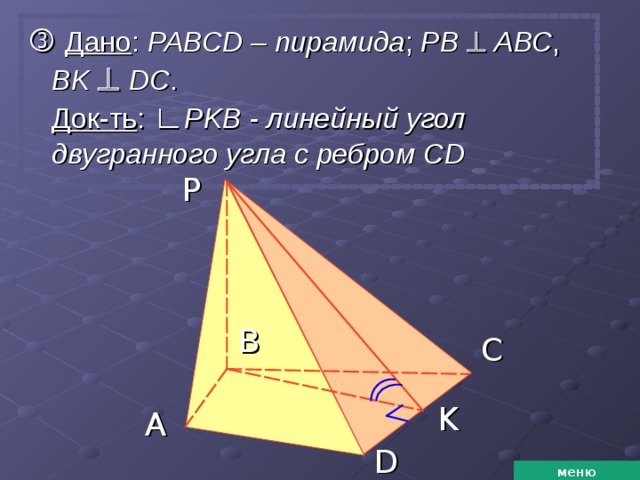
Дано : РАВС D – пирамида ; РВ АВС , В K D С . Док-ть : ∟ Р KB — линейный угол двугранного угла с ребром CD
B
C
K
A
D
меню

Вторая группа
меню
Дано : РАВС – пирамида; ∆ АВС – правильный треугольник .
Найти : Линейный угол двугранного угла с ребром АС
b) M – середина АС;
ON װ BM, PO АВС
Если:
а) D – середина АС;
PB АВС
P
P
C
A
D
N
D
B
B
M
C
A
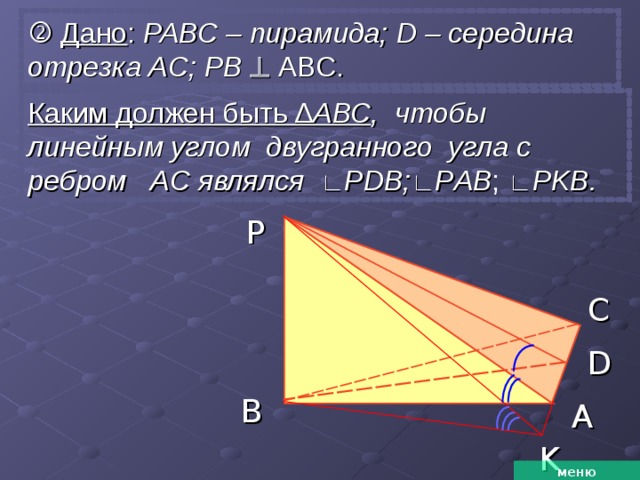
Дано : РАВС – пирамида; D – середина отрезка AC; PB ABC.
Каким должен быть ∆ АВС , чтобы линейным углом двугранного угла с ребром AC являлся ∟ Р DB; ∟ Р AB ; ∟ Р KB.
P
C
D
B
A
K
меню

Третья группа
меню
Построить линейный угол двугранного угла с ребром АС, если в пирамиде РАВС:
b) АВС – правильный ∆; О – точка пересечения медиан; PO ABC
а) AB = BC; PB ABC .
- АВС – правильный ∆; О – середина АВ; PO ABC
P
P
P
A
A
A
O
C
O
B
B
B
C
C
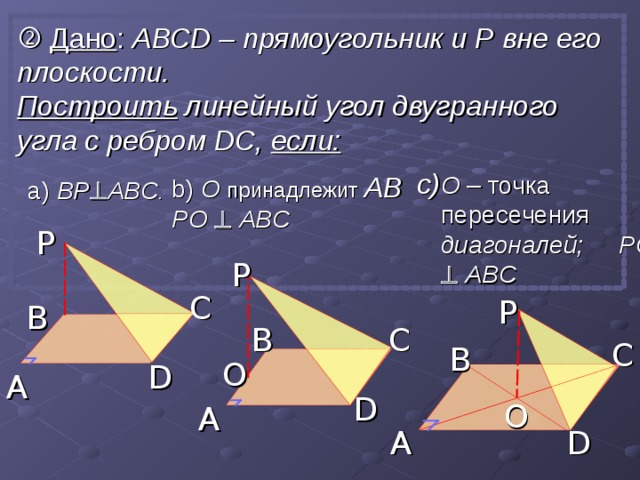
Дано : АВС D – прямоугольник и P вне его плоскости.
Построить линейный угол двугранного угла с ребром D С, если:
b) О принадлежит AB PO ABC
- О – точка пересечения диагоналей; PO ABC
а) BP ABC .
P
P
C
P
B
B
C
C
B
O
D
A
D
O
A
A
D
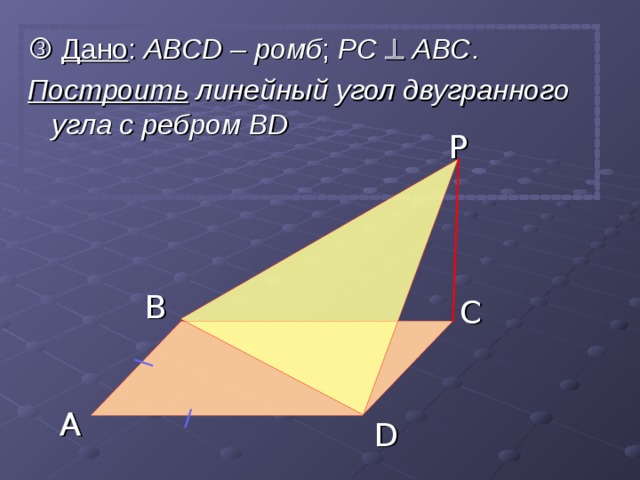
Дано : АВС D – ромб ; РС АВС .
Построить линейный угол двугранного угла с ребром В D
P
B
C
A
D
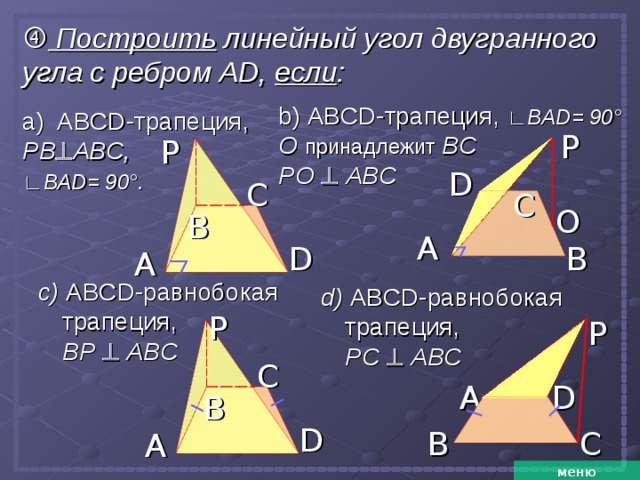
Построить линейный угол двугранного угла с ребром А D , если :
b) ABCD- трапеция, ∟ BAD = 90 ° О принадлежит B С PO ABC
а) ABCD- трапеция, PB ABC , ∟ BAD = 90 ° .
P
P
D
C
C
O
B
A
D
B
A
c) ABCD- равнобокая трапеция, BP ABC
d) ABCD- равнобокая трапеция, PC ABC
P
P
C
D
A
B
D
C
B
A
меню

Четвертая группа
меню
Дано : РАВС – пирамида .
Найти : Величину двугранного угла с ребром АС, если :
P
P
b) PO ABC , AB=BC= 5 см, BP=AC= 6 см.
а) PB ABC , BC=PB=4 см, ∟ C = 90 °
A
B
B
A
C
C
d) АВС – правильный ∆, О – середина АВ, PO ABC , AB=6 см, OP=4 см.
C ) АВС – правильный ∆, О – точка пересечения медиан, OP ABC , AB=6 см, OP=4 см.
P
P
A
A
O
B
O
B
C
C
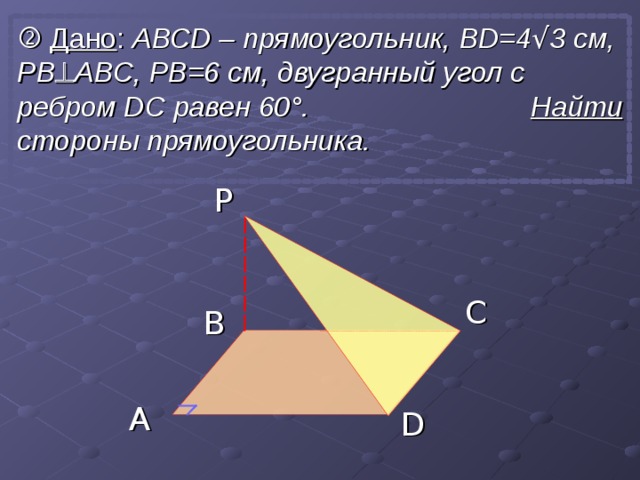
Дано : АВС D – прямоугольник, BD= 4 √ 3 см, P B ABC , PB=6 см, двугранный угол с ребром D С равен 60 ° . Найти стороны прямоугольника.
P
C
B
A
D
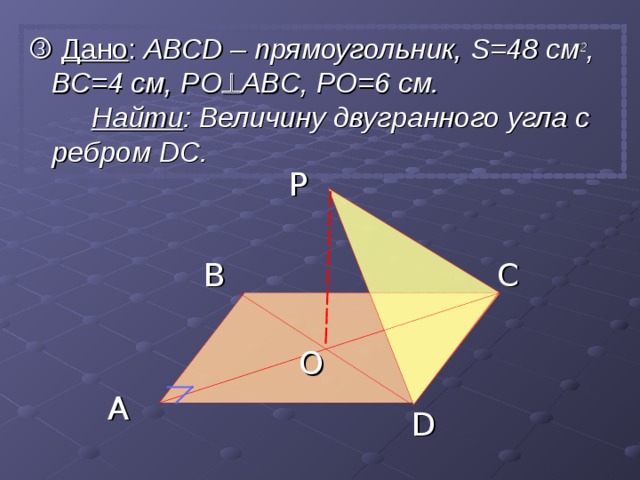
Дано : АВС D – прямоугольник, S =48 см 2 , ВС=4 см, PO ABC , PO=6 см. Найти : Величину двугранного угла с ребром DC .
P
B
C
O
A
D
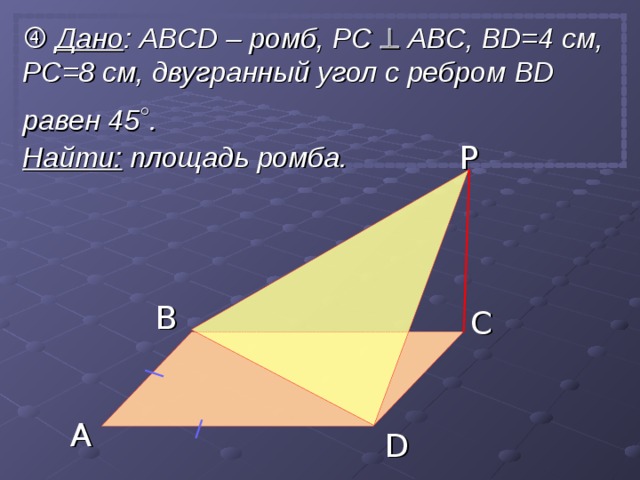
Дано : АВС D – ромб, РС АВС, BD=4 см, PC=8 см, двугранный угол с ребром BD равен 45 ° . Найти: площадь ромба.
P
B
C
A
D
15
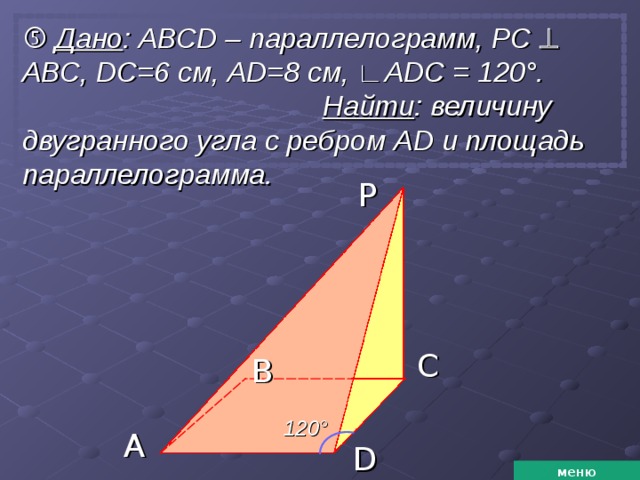
Дано : АВС D – параллелограмм, РС АВС, D С = 6 см, AD=8 см, ∟ ADC = 12 0 ° . Найти : величину двугранного угла с ребром AD и площадь параллелограмма.
P
C
B
120 °
A
D
меню

При создании презентации использована статья «Система задач по теме «Двугранные углы»» М.В.Севостьянова (г.Мурманск), журнал Математика в школе 198… г.