Название предмета: геометрия
Класс: 8
Тема урока: «Решение задач на применение признаков подобия треугольников»
Цель урока: формирование у учащихся навыков применения признаков подобия при решении задач
Задачи урока:
Образовательные: повторить признаки подобия треугольников, отрабатывать навыки их применения при решении задач.
Развивающие: активизация познавательной деятельности учащихся через решение практических задач, умение выбирать правильное решение, лаконично излагать свои мысли, анализировать и делать выводы.
Воспитывающие: организация совместной деятельности, воспитание у учащихся интереса к предмету, доброжелательности, умения выслушивать ответы товарищей.
Планируемые результаты:
Предметные: умеют демонстрировать знание основных понятий, применять признаки подобия для решения основных и качественных задач, контролировать процесс и результат учебной математической деятельности.
Познавательные: осуществляют поиск информации для выполнения учебных заданий
Регулятивные: умеют адекватно оценивать правильность или ошибочность выполнения учебной задачи, её объективную трудность и собственные возможности её решения, контролировать действия партнёра, осуществлять самоаналаз и самоконтроль.
Коммуникативные: вступают в речевое общение, участвуют в диалоге.
Личностные: проявляют познавательный интерес к изучению предмета
Техническое обеспечение урока:
Компьютер, плазменная панель, электронная презентация, выполненная в программе Power Point
Дополнительное методическое и дидактическое обеспечение урока: лист оценки знаний, карточки с готовыми чертежами для парной работы, текст задач из ОГЭ для классной работы, тест, карточки для индивидуальной работы, набор карточек для домашней работы.
Содержание урока:
1.Этап мотивации к учебной деятельности.
2. Целеполагание и мотивация.
3. Актуализация знаний.
4.Формирование практических навыков.
5. Воспроизведение знаний на новом уровне (дифференцированная работа)
6. Подготовка учащихся к обобщающей деятельности.
7. Итог урока.
8. Домашнее задание
Ход урока:
1.Этап мотивации к учебной деятельности.
(слайд 2) Учитель:
Геометрия полна приключений, потому, что за каждой задачей скрывается
приключение мысли. Решить задачу – это значит пережить приключение.
В. Произволов
— Я желаю вам сегодня интересных приключений. А маршрут наших сегодняшних приключений представлен на листе оценки знаний. Они у вас у каждого на парте зелёного цвета. на каждом этапе урока вы будете оценивать в баллах результат ваших приключений. Критерии оценивания каждого этапа тоже представлены на этом листе.
Лист оценки знаний (Приложение 6)
2. Целеполагание и мотивация.
Треугольник – самая простая геометрическая фигура, знакомая нам с детства. К треугольнику на уроках геометрии мы обращаемся чаще всего. Эта фигура таит в себе немало интересного и загадочного, как Бермудский треугольник, в котором бесследно исчезают корабли и самолеты. Один мудрец сказал: “Высшее проявление духа – это разум. Высшее проявление ума – это геометрия. Клетка геометрии – это треугольник. Он так же неисчерпаем, как и Вселенная”. Это одна из основных фигур школьного курса планиметрии. Подобие, наряду с равенством треугольников, является одним из важнейших геометрических отношений. Если равенство объектов мы понимаем как «одинаковость» и по форме, и по размеру, то подобие объектов означает их « одинаковость» только по форме. Умение решать задачи на применение признаков подобия широко используется в геометрии, физике, астрономии.
— Вспомним, какие новые понятия, утверждения, теоремы вы изучали на последних предыдущих уроках? (подобные треугольники, пропорциональные отрезки, коэффициент подобия, отношение площадей, признаки подобия треугольников)
— То есть вы уже готовы прямо сейчас решать контрольную работу по данной теме? (нет)
— Почему? (не до конца усвоена тема, мало решали задач на применения признаков подобия и т.д.)
— Значит, какую цель поставите перед собой на уроке? (тренировка, решать задачи, применение признаков подобия при решении задач и т.д.)
— Отлично, то есть сегодня на уроке мы будем применять признаки подобия при решении задач, в частности, задач практической направленности, которые встречаются в ОГЭ.
— Откройте тетради, запишите число, тему урока: Решение задач на применение признаков подобия треугольников.
3. Актуализация знаний.
3.1 Проверка домашнего задания.
Чтобы урок прошел успешно, надо повторить теоретический материал. Но сначала проверим, как вы справились с домашним заданием.
Проверка домашнего задания (самопроверка). 2 ученика по очереди комментируют домашние задачи, чертежи к которым заранее приготовлены на доске. После самопроверки по критериям, данным в оценочном листе ребята ставят себе баллы за этот этап работы)
3.2 Проверка усвоения теоретических знаний: определения подобных треугольников, признаков подобия треугольников, (слайд 4,5) . На экране последовательно появляются утверждения, истинность или ложность которых нужно установить.
Верно ли утверждение:
Два треугольника подобны, если их углы соответственно равны и сходственные стороны пропорциональны. (да)
Два равносторонних треугольника всегда подобны. (да)
Если три стороны одного треугольника соответственно пропорциональны трем сторонам другого треугольника, то такие треугольники подобны. (да)
Стороны одного треугольника имеют длины 3, 4, 6 см, стороны другого треугольника равны 9, 14, 18 см. Подобны ли эти треугольники? (нет)
Периметры подобных треугольников равны. (нет)
Если два угла одного треугольника равны 60° и 50°, а два угла другого треугольника равны 50° и 80°, то такие треугольники подобны. (нет)
Два прямоугольных треугольника подобны, если имеют по равному острому углу. (да)
Два равнобедренных треугольника подобны. (нет)
Если два угла одного треугольника соответственно равны двум углам другого треугольника, то такие треугольники подобны. (да)
Если две стороны одного треугольника соответственно пропорциональны двум сторонам другого треугольника, то такие треугольники подобны. (нет)
Даётся время для выбора ответа. Каждый записывает в тетради « ДА» или «НЕТ» в зависимости от того, считает утверждение верным или нет. После того как ответ записан сразу происходит обсуждение, ребята сравнивают свой вариант ответа с правильным и отмечают + или — . По окончании количество набранных баллов фиксируется в листе оценки знаний.
4.Формирование практических навыков.
4.1 Третий лишний(слайд 6,7,8,9)(Приложение 1)
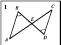
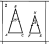
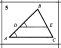
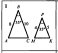

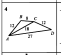
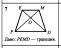
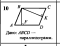
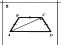
Ребята работают в парах и ищут, какая пара треугольников является лишней в каждом ряду и почему. Задание выполняется фиксированное количество времени – 4 мин. После того как время вышло, проверяем полученные результаты. Происходит подсчёт баллов в соответствии с критериями в листе оценки знаний.
Ответ: 1 ряд – 2, т.к.на 1 и 5 чертежах треугольники подобны по двум углам;
2 ряд — 1, т.к.на 3 и 4 чертежах треугольники подобны по трём сторонам;
3 ряд — 5, т.к.на этом чертеже нет подобных треугольников.
4.2 Решении задач ОГЭ
— Ребята, давайте применим наши знания по теме «Подобие треугольников» при решении задач ОГЭ. У каждого ученика на парте лежит текст задач ОГЭ.
Задачи из ОГЭ. (слайд 10,11,12,13) (Приложение 2)
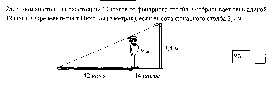
— Нельзя ли перевести эту реальную ситуацию на математический язык?
— Постройте геометрическую модель этой задачи.
— Начертите рисунок в тетрадь, введите обозначения и запишите, что дано, что требуется найти.
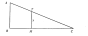
Дано: ABВС, ТМВC, АВ=2,4м, СМ = 42 ш, МС = 14 ш,
Найти: ТМ.
Поиск решения задачи:
— Что нам надо найти? ТМ
— Что достаточно знать, чтобы найти ТМ? Установить, что ∆ АВС подобен ∆ ТМС
— Как можно установить подобие треугольников? По двум углам
— Что следует из подобия? Отношение сходственных сторон 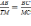
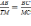
— Сможем мы найти из этого отношения искомую величину? Сможем
— План решения понятен? Повторите.
План решения задачи:
— устанавливаем подобие треугольников ∆ АВС и ∆ ТМС;
— Составляем отношение сходственных сторон;
— подставляем известные величины;
— решаем пропорцию, находим ТМ.
Ученик выходит к доске, оформляет решение этой задачи. Остальные у себя в тетрадях.
Ответ:1,8
Задача 2. В параллелограмме ABCD AE – биссектриса угла А. Стороны параллелограмма АВ и ВС относятся как 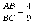 . АЕ пересекает диагональ BD в точке К. Найти отношение
. АЕ пересекает диагональ BD в точке К. Найти отношение 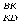 .
.
— Прочитайте задачу. Что дано в задаче?- Что нужно найти?
— Давайте сделаем чертеж к задаче (один человек работает у доски).
— Что такое биссектриса угла?
— Обозначим равные углы. Напишем дано, что надо найти.
Д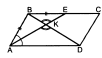 ано: ABCD – параллелограмм, AE – биссектриса,
ано: ABCD – параллелограмм, AE – биссектриса, 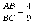 .
.
Найти: 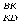 .
.
Поиск решения задачи: — Что нам надо найти? 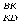
— Откуда найдем отношение сторон? ∆ ВКЕ и ∆DКА
— Что будем делать с треугольниками? доказывать подобие
— Что для этого достаточно доказать? 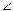 BКЕ=
BКЕ=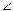 DКА – как вертикальные
DКА – как вертикальные
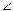 ВЕА=
ВЕА=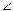 ЕАD (
ЕАD (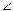 EBD=
EBD=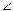 BDA)(как накрест лежащие при прямых ВС и АD и секущей АЕ(ВD))
BDA)(как накрест лежащие при прямых ВС и АD и секущей АЕ(ВD))
— По какому признаку установили подобие? (по 1 признаку)
— Что следует из подобия? (пропорциональность сходственных сторон 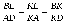 )
)
— Как связать сторону АВ с нашими подобными треугольниками? рассмотреть ∆АВЕ
— Каким является этот треугольник? равнобедренным (углы при основании равны, АВ=ВЕ)
— Что следует из этого равенства? 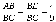 ,
, 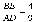 (т.к. ВС=АD)
(т.к. ВС=АD)
— Что можно найти из равенства 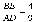 ? (коэффициент подобия k=
? (коэффициент подобия k= )
)
— Как найти 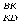 ?
? 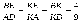
— План решения понятен? Повторите.
План решения задачи:
— устанавливаем подобие треугольников ∆ ВКЕ и ∆ DКА;
— доказательство подобия, через равные углы при параллельных прямых и секущей;
— устанавливаем соотношение сходственных сторон в подобных треугольниках;
— рассматриваем равнобедренный ∆АВЕ, устанавливаем равенство сторон;
— находим коэффициент подобия;
— выявляем отношение 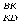 .
.
— Ученик оформляет решение у доски, на обороте, остальные самостоятельно, потом сверяем.
Решение:
1. 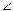 BКЕ=
BКЕ=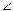 DКА – как вертикальные;
DКА – как вертикальные; 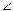 ВЕА=
ВЕА=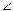 ЕАD (
ЕАD (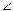 EBD=
EBD=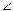 BDA) (как накрест лежащие при прямых ВС и АD и секущей АЕ(ВD))= ∆ ВКЕ и ∆ DКА подобные (по 1 признаку);
BDA) (как накрест лежащие при прямых ВС и АD и секущей АЕ(ВD))= ∆ ВКЕ и ∆ DКА подобные (по 1 признаку);
2. ∆ ВКЕ и ∆ DКА подобные =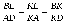 ;
;
3. расм-м ∆АВЕ: 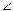 ВЕА=
ВЕА=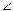 ЕАD,
ЕАD, 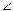 ВАЕ=
ВАЕ=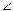 DАЕ (т.к. АЕ – биссектриса) = ∆АВЕ – равнобедренный;
DАЕ (т.к. АЕ – биссектриса) = ∆АВЕ – равнобедренный;
4. ∆АВЕ – равнобедренный, АВ=ВЕ = устанавливаем 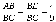 ;
;
5. ВС=АD (противоположные стороны в параллелограмме) = 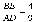 ;
;
6. 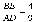 = коэффициент подобия k=
= коэффициент подобия k= ;
;
7. 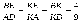 , т.е.
, т.е. 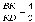 .
.
Ответ: 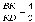 .
.
— Попробуйте сформулировать свойство биссектрисы угла параллелограмма. Что она сделала с параллелограммом?
Свойство биссектрисы параллелограмма: Биссектриса угла параллелограмма отсекает от него равнобедренный треугольник.
— Запишите себе это свойство, вы им можете пользоваться и при решении других задач.
5. Воспроизведение знаний на новом уровне (дифференцированная работа)
1. Работа в парах. Тест. (слайд 14) (Приложение 3)
|
|
1 вариант |
2 вариант |
|
1 |
Б |
А |
|
2 |
В |
А |
|
3 |
Б |
А |
|
4 |
Б |
Б |
|
5 |
А |
А |
Я предлагаю Вам небольшой тест, проверьте каждый сам себя, как хорошо вы изучили тему. В тесте 5 вопросов, внимательно прочтите сначала вопрос, затем предложенные ответы и лишь потом подчеркните ответ, который вы считаете правильным. (Приложение 2.) Самопроверка.
Критерии оценок: по 1 баллу-«1 и 2 задания », по 2 балла – «3 – 5 задания ».
2. Индивидуальная работа по карточкам (Приложение 4.)
6. Подготовка учащихся к обобщающей деятельности.
В геометрии подобными могут быть не только треугольники, но и совершенно произвольные фигуры. На слайде мы видим подобные игрушки, подобные растения. (слайды 15, 16,17)
Как вы думаете, какими свойствами они все обладают? [ У них одинаковые формы, но разные размеры]
Пропорциональность проявляется везде: в подобном строении дерева и его ветвей, в форме снежинок и кристаллов. Стекло и хрусталь состоят из мельчайших частиц, кристаллов. Поверхность хрустальной вазы состоит из геометрических фигур, которые подобны друг другу.
7. Итог урока.
Пришло время подвести итог.
Подсчитайте количество набранных баллов и по критерию, представленном на оценочном листе переведите их в оценки.
Выше 22 баллов – 5;17 -21 баллов – 4;12 — 16 баллов – 3;0 -11 баллов — 2
Поставьте себе отметку в оценочный лист.
— Для утверждения оценок я прошу передать тетради вместе с оценочными листами и тестами. Каждый за сегодняшний урок получит оценку. По предварительным данным кто получил 5, 4, 3,2,1?
-Кроме того за работу на уроке при решении задач получают оценки …
— Достигли ли мы цели, поставленной нами в начале урока?
Используя схему на слайде, ответьте на вопросы: (слайд 18)
Сегодня на уроке я повторил…
Сегодня на уроке я научился? …
Мне необходимо ещё поработать над…..
8. Домашнее задание
Всем удачи, спасибо за урок. (слайд 20)