Обобщающий урок по теме «Простейшие тригонометрические уравнения»
10 класс, УМК под ред. Мордковича А.Г.
Цели: 1) обобщить знания учащихся о формулах корней простейших тригонометрических уравнений; формировать умение решать простейшие тригонометрические уравнения;
2) развивать логическое мышление учащихся;
3) воспитывать культуру труда.
Ход урока
I. Организационный момент. Выяснение вопросов по домашнему заданию.
II. Проверочная работа.
Вариант 1
1. Вычислите.
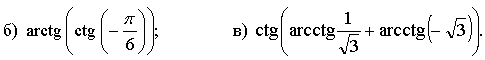
2. Решите уравнение.
Вариант 2
1. Вычислите.
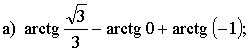
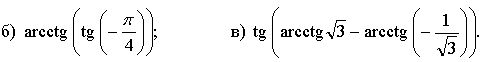
2. Решите уравнение.
III. Объяснение нового материала.
План объяснении нового материала.
-
Какие тригонометрические уравнения называются простейшими.
-
Какие существуют формулы корней для решения простейших тригонометрических уравнений.
-
Частные случаи решения простейших тригонометрических уравнений.
-
Как решать простейшие тригонометрические уравнения, в которых под знаком тригонометрической функции стоит выражение вида kx + m.
-
Примеры решения простейших тригонометрических уравнений и нахождение их корней на заданном промежутке.
IV. Формирование умений и навыков.
Решение упражнений по направлениям:
1) отработка формул корней простейших тригонометрических уравнений;
2) нахождение корней простейших тригонометрических уравнений на заданном промежутке.
1-я группа.
1. № 18.1, № 18.2, № 18.3.
2. № 18.5 (а; б).
Решение:
Для решения подобных уравнений сначала следует воспользоваться формулами приведения.
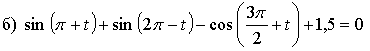
2-я группа.
1. № 18.14 (б).
2. № 18.15 (а; в).
3. № 18.19.
Решение:
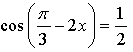
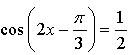
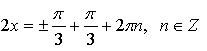
а) При 
то есть 
то есть
– наименьший положительный корень;
б) при 
при 
при 
Ответ: 
в) при 
– наибольший отрицательный корень.
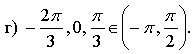
Дополнительно можно предложить учащимся задание № 18.16.
Решение:
при 
при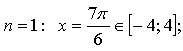 
при 
при 
при 
Ответ: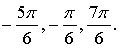 
V. Итоги урока.
– Какие тригонометрические уравнения называются простейшими?
– Назовите формулы корней для решения уравнений: sin х = а,
cos х = а, tg x = а, ctg x = а.
– Какие существуют частные случаи решения простейших тригонометрических уравнений?
– Как решить уравнение, в котором под знаком тригонометрической функции стоит выражение вида kx + m?
– Как находить корни тригонометрического уравнения на заданном промежутке?
Домашнее задание: № 18.4, № 18.5 (в; г), № 18.15 (б; г), № 18.18.
Дополнительно: № 18.17.
