
Задачи на геометрическое место точек
Геометрия. Глава IV. §4
Сарычев П. А.
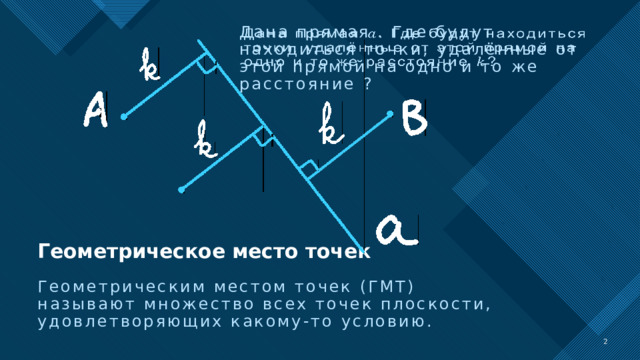
Дана прямая . Где будут находиться точки, удалённые от этой прямой на одно и то же расстояние ?
Геометрическое место точек
Геометрическим местом точек (ГМТ) называют множество всех точек плоскости, удовлетворяющих какому-то условию.
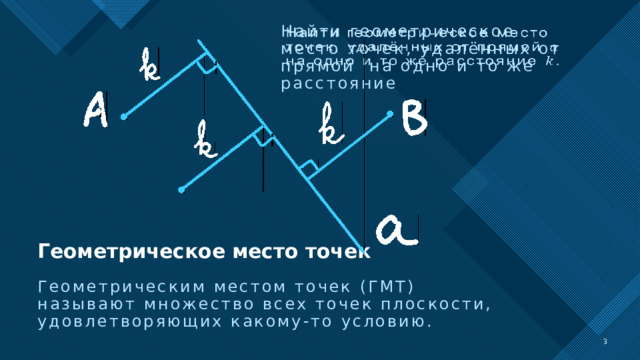
Найти геометрическое место точек, удалённых от прямой на одно и то же расстояние
Геометрическое место точек
Геометрическим местом точек (ГМТ) называют множество всех точек плоскости, удовлетворяющих какому-то условию.

Найти геометрическое место точек, удалённых от прямой на одно и то же расстояние
Проведём прямые и так, чтобы причём
I. Все точки, удалённые от прямой на расстояние , лежат на прямых и
Если , то или
II. Все точки прямых и удалены от прямой на расстояние
Если или , то

Даны параллельные прямые a и b. Найти геометрическое место середин отрезков, соединяющих точки, лежащие на прямых a и b соответственно.
Гипотеза. ГМТ – все точки прямой , параллельной прямым и и равноудалённой от них.

Даны параллельные прямые a и b. Найти геометрическое место середин отрезков, соединяющих точки, лежащие на прямых a и b соответственно.
- Дано: – сер. , ,
Доказать: .
1) Проведём перпендикуляры к и к . Тогда
2) Рассмотрим и – п/уг
1) (т.к. – сер. )
2) (как накрест леж. при и секущей )
Следовательно, по гипотенузе и острому углу.
3) (т.к. ), т.е.

Даны параллельные прямые a и b. Найти геометрическое место середин отрезков, соединяющих точки, лежащие на прямых a и b соответственно.
- Дано: .
Доказать: – сер. , где .
1) Проведём перпендикуляры к и к . Тогда .
2) (т.к. )
3) (как накрест леж. при и секущей )
4) (как односторонние при и секущей )
5) . Следовательно, и – сер.

Решение задач на ГМТ
Чтобы найти множество всех точек, удовлетворяющих данному условию, нужно:
- Сформировать гипотезу, какой фигурой является это множество точек;
- Доказать, что если точка удовлетворяет данному условию, то она принадлежит фигуре;
- Доказать, что если точка принадлежит фигуре, то она удовлетворяет данному условию;
- Сделать вывод.

Домашнее задание
- Из точки к прямой проведены наклонные и и перпендикуляр так, что луч проходит внутри угла Сравните отрезки и , если
- Даны точки и . Найти геометрическое место точек, удаленных от и на одно и то же расстояние .